Representación binomial de un número complejo en términos de parte real y parte imaginaria. Fuente: Pixabay. Ejemplos de números complejos son 2 – 3i, -πi, 1 + (1/2)i. Pero antes de operar con ellos, vamos a ver de dónde se origina la unidad imaginaria i, considerando esta ecuación cuadrática: x2 – 10x + 34 = 0. En la cual a = 1, b.. Aprende gratuitamente sobre matemáticas, arte, programación, economía, física, química, biología, medicina, finanzas, historia y más. Khan Academy es una organización sin fines de lucro, con la misión de proveer una educación gratuita de clase mundial, para cualquier persona en cualquier lugar.

OPERACIONES CON NÚMEROS COMPLEJOS YouTube

Los Números Complejos Math4all

Calaméo Mapas Conceptuales Números Complejos

Números Complejos Fórmulas y Explicaciones Matemáticas álgebra YouTube

Números complejos YouTube

¿Qué son los números complejos? YouTube

Números Complejos Parte 1 YouTube
Los Números Complejos Math4all
Los Números Complejos Math4all

NúMeros Complejos

Tipos de Números Complejos para Quinto Grado de Secundaria

Propiedades de numeros complejos UDOE

PPT Los Números Complejos PowerPoint Presentation, free download ID849665

¿Cuáles son los 3 tipos de número complejo? Apolonio.es

blogartesvisuales

Clasificación y Operaciones con Números Complejos para Cuarto Grado

Clasificación de los Números Complejos , Imaginario Puro , Complejo Real , Unidad Imaginaria

Números complejos y sus representaciones. Álgebra, Números, Aprendizaje

Números COMPLEJOS RESUMEN con ejemplos y ejercicios (con soluciones!!)
Resumen de numeros complejos Superprof
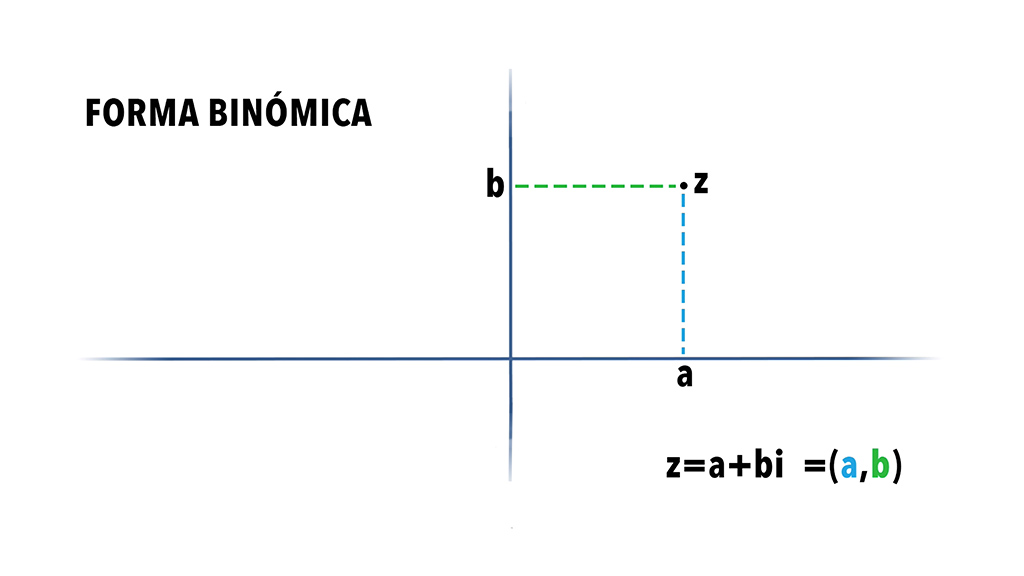
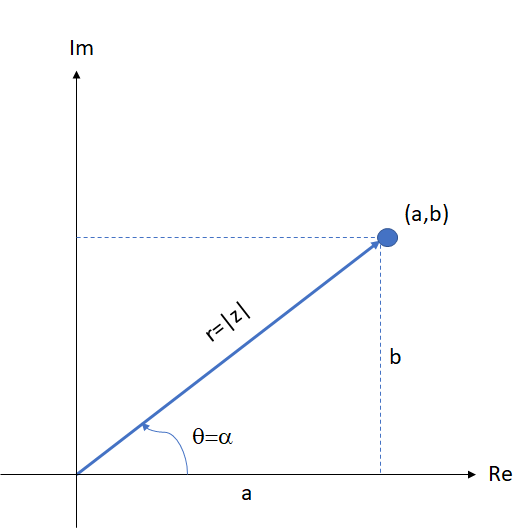
Aunque muy poderosos, los números reales son inadecuados para resolver ecuaciones como \(x^2+1=0\), y aquí es donde entran los números complejos.Definimos el número \(i\) como el número imaginario tal que \(i^2 = -1\), y definimos números complejos como los de la forma \(z = a + bi\) donde \(a\) y \(b\) son números reales. A esto lo llamamos la forma estándar, o forma cartesiana, del.. Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra , o en forma polar ).




